拓扑结构有哪几种类型？它们各自的特点是什么？

拓扑学作为数学中的一个重要分支，研究的是空间的形状和连通性。拓扑学的研究对象可以是任意维度的空间，从点、线、面到更复杂的结构都有涉及。本文将介绍拓扑学中几种常见的拓扑结构类型，并探讨其在不同领域的应用。

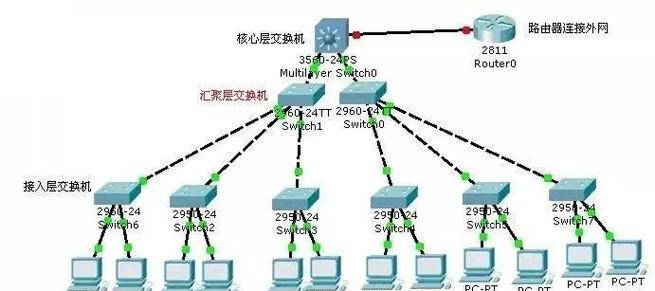
1.点拓扑结构的基本特征与应用

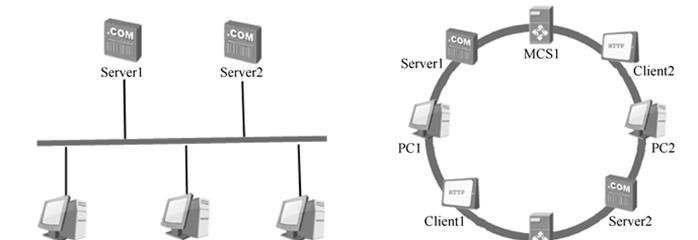
点拓扑结构是拓扑学中最基本的结构之一，它研究的是离散点之间的关系和连通性。在计算机科学中，点拓扑结构被广泛应用于图论和网络拓扑的研究中。

2.线拓扑结构的特性及其在物理学中的应用

线拓扑结构是由一条连续曲线构成的结构，它关注的是曲线上各个点之间的关系。在物理学领域，线拓扑结构被用于描述凝聚态物质中的电子行为以及拓扑绝缘体等现象。

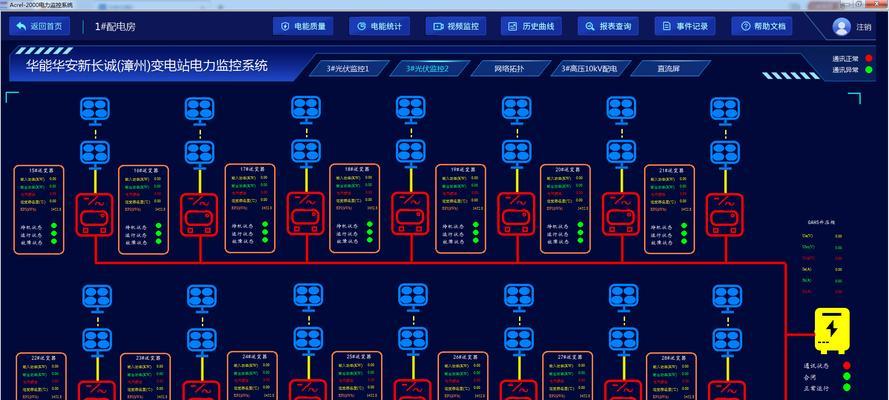
3.面拓扑结构的性质与地理学中的应用

面拓扑结构由一个平面或曲面所构成，研究的是平面或曲面上各个点的关系。在地理学中，面拓扑结构被用于描述地球表面的地貌特征、地势起伏等。

4.点线面之外：高维拓扑结构的探索与发展

除了点、线、面这些常见的拓扑结构外，高维拓扑结构也是拓扑学研究的重要方向之一。本节将介绍高维拓扑结构的特点以及在数据分析、神经科学等领域中的应用。

5.拓扑学在网络安全中的应用

拓扑学在网络安全中起到了重要的作用。本节将介绍如何利用拓扑学的方法来分析和优化网络拓扑结构，以提高网络的安全性和稳定性。

6.拓扑学在生物学中的应用

生物学中许多复杂的生物体结构可以通过拓扑学的方法进行研究和描述。本节将介绍如何利用拓扑学的工具来研究DNA的结构、蛋白质折叠等生物学问题。

7.拓扑学在城市规划中的应用

城市规划中的交通网络、供电网络等可以被视为拓扑结构。本节将介绍如何利用拓扑学的方法来优化城市规划，提高城市的可持续发展能力。

8.拓扑学在化学反应网络中的应用

化学反应网络中的反应物和产物之间的关系可以通过拓扑学的方法进行分析。本节将介绍如何利用拓扑学的工具来研究和优化化学反应网络，提高反应效率和选择性。

9.拓扑学在计算机网络中的应用

计算机网络中的节点和连接关系可以被视为拓扑结构。本节将介绍如何利用拓扑学的方法来分析和优化计算机网络，提高网络性能和可靠性。

10.拓扑学在信号处理中的应用

信号处理中的信号流动关系可以通过拓扑学的方法进行建模和分析。本节将介绍如何利用拓扑学的工具来处理和优化信号，提高信号处理的效果。

11.拓扑学在金融网络中的应用

金融网络中的各个金融机构之间的关系可以被视为拓扑结构。本节将介绍如何利用拓扑学的方法来分析和优化金融网络，提高金融系统的稳定性。

12.拓扑学在社交网络中的应用

社交网络中人与人之间的联系可以被视为拓扑结构。本节将介绍如何利用拓扑学的方法来分析和优化社交网络，发现社区结构和影响力节点等。

13.拓扑学在图像处理中的应用

图像处理中的像素点之间的关系可以通过拓扑学的方法进行建模和分析。本节将介绍如何利用拓扑学的工具来处理和优化图像，提高图像处理的效果。

14.拓扑学在物联网中的应用

物联网中各个物联设备之间的关系可以被视为拓扑结构。本节将介绍如何利用拓扑学的方法来分析和优化物联网的拓扑结构，提高物联网的可靠性和安全性。

15.拓扑学的未来发展与挑战

本文最后一节将拓扑学的研究进展，并探讨拓扑学未来的发展方向和面临的挑战，展望拓扑学在各个领域的广泛应用前景。

本文从点、线、面等基本拓扑结构类型出发，介绍了拓扑学在不同领域的应用。通过深入探索拓扑学的奥秘，我们可以更好地理解和优化各种拓扑结构，推动各个领域的发展。拓扑学作为一门富有潜力的学科，将继续在未来的研究中发挥重要作用。