快速幂运算步骤解析（快速幂算法的原理）

电脑技巧 2024年10月31日 10:24 24 游客

快速幂运算是一种高效计算指数幂的算法，它通过将指数拆解为二进制形式的位运算，大大减少了计算次数，提高了运算效率。本文将详细解析快速幂运算的步骤，讨论其原理、应用以及相关的优化方法。

快速幂运算步骤解析（快速幂算法的原理）

基本概念与原理

1.1快速幂运算的定义与作用

快速幂运算是一种通过对指数进行拆解和位运算来加速求幂运算的方法，主要用于计算大数的指数幂。

1.2基本步骤及思想

快速幂运算的基本步骤包括指数拆解、位运算以及累乘计算。其核心思想是利用指数的二进制表示形式，通过不断平方和累乘计算得到最终结果。

快速幂运算的应用

2.1指数幂运算

快速幂运算广泛应用于指数幂的计算，特别适用于大数的幂运算，如计算2的n次幂。

2.2模幂运算

在密码学和数据加密领域，模幂运算是一种重要的算法，利用快速幂运算可以高效计算大数的模幂。

2.3矩阵幂运算

快速幂运算也可以应用于矩阵幂的计算，通过对矩阵进行快速幂运算，可以快速求解复杂的线性方程组。

优化方法与技巧

3.1指数二进制展开

快速幂运算中，将指数转化为二进制形式是关键一步，可以通过指数的二进制展开来实现，减少了计算的次数。

3.2递归与迭代优化

在实际应用中，可以使用递归和迭代的方式来优化快速幂运算的效率，避免重复计算和内存溢出的问题。

3.3模运算优化

对于模幂运算，采用取模运算的方式可以大大减少计算量，提高运算速度和精度。

案例分析与实例演示

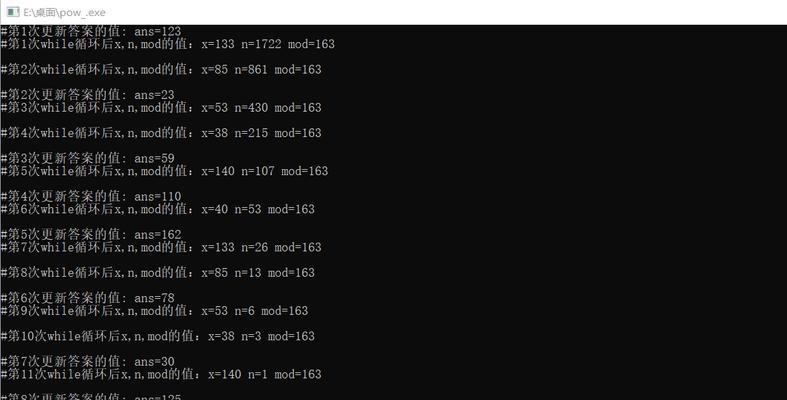
4.1计算2的n次幂的实例演示

通过具体的实例演示，详细解析快速幂运算在计算2的n次幂上的应用和效果。

4.2计算大数模幂的案例分析

以大数模幂运算为例，分析快速幂运算在实际应用中的性能优势和实现方法。

通过对快速幂运算的步骤、原理、应用以及优化方法进行详细的解析，我们可以看到快速幂运算作为一种高效的指数幂计算方法，在各个领域都有着重要的应用价值。熟练掌握快速幂运算的步骤和优化技巧，不仅可以提高计算效率，还可以减少计算量，节省计算资源。

快速幂运算的原理与应用

在数学和计算机领域中，幂运算是一种常见且重要的计算操作。当需要计算一个数的高次方时，传统的方法往往会消耗大量时间和计算资源。而快速幂运算作为一种优化算法，可以大大提高幂运算的效率。本文将介绍快速幂运算的原理和应用，并详细阐述该算法的步骤和实现方式。

一、快速幂运算的基本原理

1.1二分思想：将幂运算逐步分解为更小规模的子问题

1.2递归思想：利用递归将子问题不断缩小至最小规模

1.3重复利用中间结果：通过记录中间结果减少重复计算

二、快速幂运算的步骤

2.1将底数递归分解为更小规模的子问题

2.2对子问题进行求解，并记录中间结果

2.3利用中间结果计算整个问题的解

2.4通过递归的方式，将子问题的解逐层返回至初始问题

三、实际应用场景

3.1数论问题：计算大数的高次方余数

3.2密码学应用：加密算法中的指数运算

3.3矩阵运算：矩阵快速幂求解

四、应用示例：计算大数的高次方

4.1输入底数和指数

4.2利用快速幂算法进行计算

4.3输出结果

五、时间复杂度分析

5.1传统幂运算的时间复杂度

5.2快速幂运算的时间复杂度

5.3对比分析两种方法的效率差异

六、空间复杂度分析

6.1传统幂运算的空间复杂度

6.2快速幂运算的空间复杂度

6.3对比分析两种方法的空间开销

七、优化思路与改进方法

7.1迭代方式实现快速幂运算

7.2取模优化：减少中间结果的大小

7.3应用位运算：进一步提升运算效率

八、注意事项与应用限制

8.1底数和指数的边界情况处理

8.2快速幂运算在特定场景下的适用性

8.3对结果的精度要求

九、

通过本文的介绍，我们了解了快速幂运算的基本原理和应用方法，并且详细讨论了该算法的步骤、时间复杂度、空间复杂度以及优化思路。掌握了快速幂运算，我们可以高效地计算大数的高次方，并在数论、密码学等领域中应用该算法。在实际应用中，我们需要注意边界情况和精度要求，选择合适的优化策略，以获得更好的计算效果。希望本文能为读者理解和应用快速幂运算提供帮助。

标签：步骤

快速幂运算步骤解析（快速幂算法的原理）

快速幂运算的原理与应用

Linux的优缺点盘点（探索Linux操作系统的优势和不足）

《平板选购万能攻略指南》（从性能到价格）

热门文章

最新文章

标签列表